快速傅里叶变换(FFT)实现了时域到频域的转换,是信号分析中最常用的基本功能之一。FFT变换时,总是从离散数据中选取一部分处理,将其称为一帧数据。而且FFT是在一定假设下完成的,即认为被处理的信号是周期信号。因此,FFT之前会对这一帧数据进行周期扩展。
以CW信号为例,如果选取的这一帧数据不是信号周期的整数倍,则在周期扩展时会存在样点的不连续性,如图1所示。这将导致FFT之后得到的频谱失真,主要体现在频率成分上。理论上,频谱中只包含待测信号的频率,但实际上此时的频谱包含众多的频率分量。通常将这种现象称为频谱泄露效应。
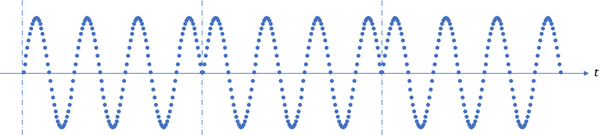
图1. 周期扩展造成样点不连续
为了抑制频谱泄露效应,可以采用诸如Hanning、Kaiser等多种时间窗。还有一种特殊的时间窗——矩形窗,其实就是不加时间窗,直接对原始样点做FFT变换,上述例子就是采用矩形窗的情况。只有采用矩形窗,而且窗宽度不是信号周期的整数倍时,才会发生明显的频谱泄露效应。
本文的重点并非介绍如何采用时间窗抑制频谱泄露效应,而是从理论上剖析采用矩形窗时造成频谱泄露的本质。
1. 为什么会造成频谱泄露?
图1所示的样点不连续也意味着相位不连续,存在180°相位反转。总体来讲,可以将其理解为相位调制,而且是一种特殊的相位调制,调制信号不是经典的正弦波信号,而是方波信号,可以将调制信号写为如下形式:
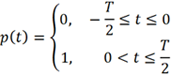
式中,T 为调制信号的周期,为一帧波形时长的两倍。这意味着在t=0 时刻,载波的相位发生了变化。
既然可以理解为相位调制,则可将已调信号写为如下形式:
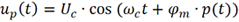
式中φm为相位偏移,对于图1的例子,φm=π。很显然,调制信号已经不再是单频点信号,而是多频点信号。对于图2所示的周期为T 的方波信号,其频谱包含DC、基波及其众多的奇次谐波分量 。
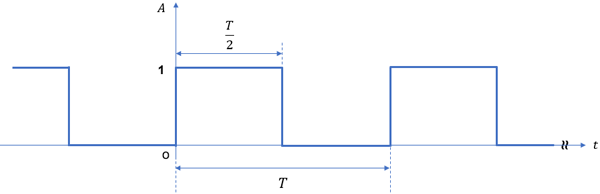
图2. 调制信号p(t)的时域波形
满足Dirichlet 条件时,任何周期函数均可以进行傅里叶级数展开,p(t) 可以写为:
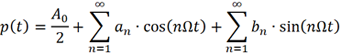
式中,Ω为方波信号的基波频率,Ω=2π/T。
经过计算,可以得到an 和bn 如下:
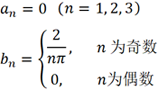
这意味着p(t) 只包含DC、基波及其奇次谐波,但阶数越高,谐波强度越弱。
可以将p(t) 重新写为:

为简便起见,首先考虑调制信号只包含DC和基波的情况,这又回到经典的相位调制。
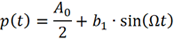
将其代入已调信号up (t) 后可得
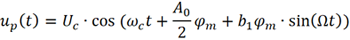
上式可以写为复指数形式
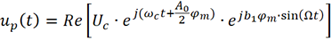
为了进一步分析,可将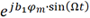 进行傅里叶级数展开,其展开式为宗数为b1φm的第一类贝塞尔函数:
进行傅里叶级数展开,其展开式为宗数为b1φm的第一类贝塞尔函数:

将其代入复指数表达式

则up (t) 可重新表示为
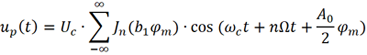
可以看出,当只考虑调制信号的DC和基波时,已调信号up (t)将包括ωc及ωc+nΩ(n为整数) 等众多频率分量。
实际中调制信号还包含丰富的谐波分量,因此对载波进行相位调制后的频谱更加丰富。面对的困难是,考虑的谐波越多,公式推导越复杂。为了简化,下面只考虑到3次谐波。
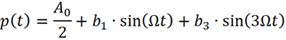
对应的已调信号为
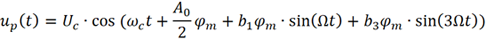
类似地,可以写为如下复指数形式
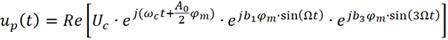
将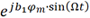 、
、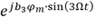 分别进行傅里叶级数展开为
分别进行傅里叶级数展开为
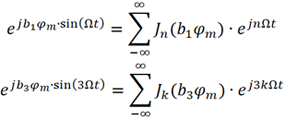
经过一番推导可得
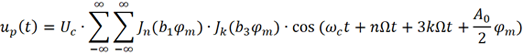
由此可见,当考虑到调制信号的三次谐波时,已调信号up (t) 的频谱更加丰富,包括ωc、ωc+nΩ 、ωc+3kΩ及ωc+nΩ+3kΩ(n,k为整数) 等众多频率分量。
以此类推,当考虑p(t) 更高阶的谐波时,将会有更多的频率项,但是从频率上看,各个频率分量都是均匀分布的,而且相邻谱线之间的间距始终为基波Ω。
2. 下面讨论一下up (t) 主要频率分量的幅度。
(1) 首先考虑载波ωc的幅度,以上面考虑到三次谐波的情况为例。当nΩt+3kΩt=0 时,对应的就是载波分量。这要求n=-3k (k 为整数),此时可以得到:
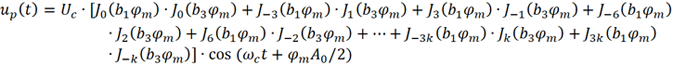
对于第一类贝塞尔函数Jn (x),其奇偶特性如下:
当n 为奇数时,Jn (x) 为奇函数;当n 为偶数时,Jn (x) 为偶函数。
进一步化简可得

因以上考虑的都是相位偏移 φm=π的情况,故b1φm=2,b3φm=2/3,代入上式得
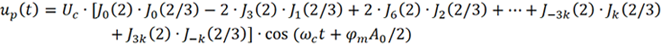
对于第一类贝塞尔函数,Jn (2)=Jn (2/3)=0 (n≥5),则
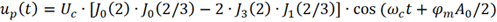
根据第一类贝塞尔函数,上式计算得到的载波信号幅度非常微弱。
(2) 频率分量ωc+Ω的幅度分析。当n=-3k+1 时,对应的就是ωc+Ω频率分量。

由于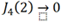 ,且Jn (2)=Jn (2/3)=0 (n≥5),上式进一步化简得
,且Jn (2)=Jn (2/3)=0 (n≥5),上式进一步化简得
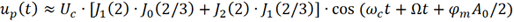
该频率分量的幅度要远远大于载波的幅度!
(3) 频率分量ωc-Ω的幅度分析。当n=-3k-1 时,对应的就是ωc-Ω频率分量。
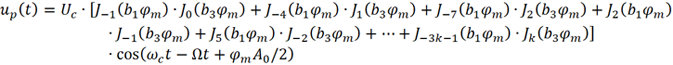
由于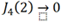 ,且Jn (2)=Jn (2/3)=0 (n≥5),上式进一步化简得
,且Jn (2)=Jn (2/3)=0 (n≥5),上式进一步化简得
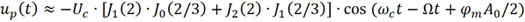
该频率分量的幅度也远远大于载波的幅度!
而且对比 ωc+Ω 和 ωc-Ω 两个频率分量,它们的幅度相同!也就是说,从频谱上看,它们是关于载波对称的!
(4) 频率分量ωc+2Ω 的幅度分析。当n=-3k+2 时,对应的就是ωc+2Ω 频率分量。
虽然(n,k) 的组合很多,但是当阶数较大时,Jn (2)= Jn (2/3)=0 (n≥5),因此可得
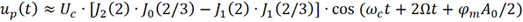
经过计算,该频率分量的幅度非常微弱。
(5) 频率分量ωc-2Ω 的幅度分析。当n=-3k-2 时,对应的就是ωc-2Ω 频率分量。
虽然(n,k) 的组合很多,但是当阶数较大时,Jn (2)= Jn (2/3)=0 (n≥5),因此可得
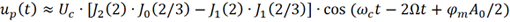
该频率分量与ωc+2Ω 的幅度相同,依然非常微弱。
上面从理论上解释了频谱泄露的起因,而且当发生频谱泄露时,会产生众多的、分布均匀的频率分量,相邻谱线的频间距取决于FFT时一帧波形的时长。
值得一提的是,相位偏移 φm不仅对各个频率分量的幅度有影响,也会影响频率分布,以后有机会再来解释这一点。
3. 通过使用AWG播放一个CW信号验证上述推导。
使用AWG 输出一个100MHz 频率的CW 信号,波形时长为10.5个周期,如图3所示,当循环播放时便可以模拟上述的相位不连续性,会造成180°的相位跳变。
对于这种波形时长不是信号周期整数倍的情况,当单次播放时,信号的频率就是100MHz ,但是当连续播放时相当于引起了相位调制,按照上述理论分析,频谱中将包含很多频率成分,图4给出了信号的实测频谱。
本例中,波形时长为105ns,这意味着频谱中相邻谱线之间的频率间隔约为:4.76MHz,这与图4所示的频谱是吻合的。
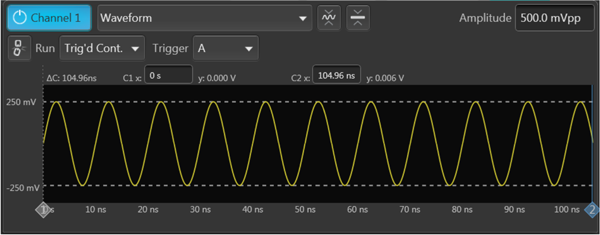
图3. 波形时长为10.5个信号周期
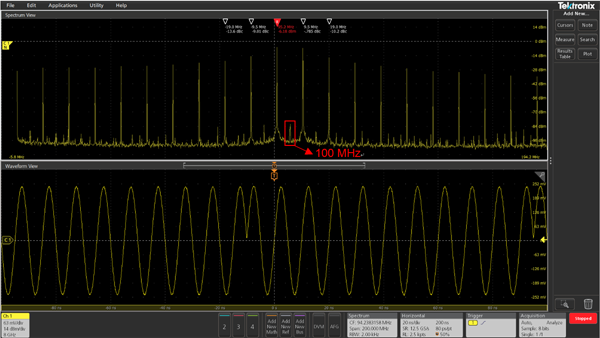
图4. 时域波形及其频谱
小结
对于使用矩形窗进行FFT时可能存在的频谱泄露效应,本文从理论上定性地进行了分析。究其原因,是因为当进行周期扩展时造成了相位的不连续。相位的不连续可以当作相位调制来处理,经过一系列推导最终解释了为什么会出现众多的频率成分。文中还对特定相位偏移情况下的频率分量的幅度进行了分析。文末通过一个实例模拟了这种相位不连续,并测试了波形和频谱,实测结果与理论推导相吻合。