如果您不是光学专业的,或者是文科生,那么您想到光的干涉和衍射第一反应应该是很多公式对不对?头好大是不是?好,那么今天我们就不用一个公式来重新解读光的干涉和衍射。
光,也叫电磁波,他的表现形式我们通常用正弦曲线来表示,如下图:

图1 电磁波曲线
光有很多物理参数,其中有一个如从A点到B点的长度我们叫做波长,波长与频率相关,即与光的颜色有关。而光波从A点走到B点,等于走了一个波长的长度,相位刚好也改变了2π,这是最基本的知识应该不用再多做介绍。好,接下来进入正题,我们来看看光的干涉是如何发生的。以图1为例,图中黑色和蓝色的电磁波,在空间发生干涉,会发生什么?刚好干涉相消;如果是蓝色和红色的电磁波发生干涉,那么就会形成一个新的幅值更高的正弦波。这里就可以简单推断出2个干涉需要满足的条件:
第一、振动方向相同,如果黑色是纸面内上下振动,蓝色如果改成垂直纸面振动,那么它俩毫无关系;
第二,频率相同以及相位差恒定,只有满足这2个条件,才能在空间中形成亮暗相间的干涉条纹。
问题来了!第一个问题,前面提到的黑色和蓝色电磁波发生干涉,刚好干涉相消,从干涉条纹来看是一片黑,即没有任何光强,也就是意味着没有能量了?这是不是违背了能量守恒定律?答案当然是不违背的。其实我们分析的都只是电场分量,而真正光的形式是这样的,能量不仅只有电场,还有磁场的:

图2 电磁波传播形式(向左)
好,现在分为二种情况分析刚才的干涉相消:对向而行和同向而行;先分析对向而行,结合图2和图3(传播方向相反),如果要让干涉相消,即电场矢量方向相反,那么我们就会发现磁场分量的振动方向是相同的,所以电场分量干涉相消,其实是把电场的能量全部转移到磁场上去了,所以总能量依旧是守恒的。

图3 电磁波向右传播
接下来分析同向而行的情况,如果你用上面的方式套用的话,你会发现电场矢量干涉相消,磁场也干涉相消,能量真的消失了?不是,原因在什么地方?继续举例子,看图说话:

图4 电磁波干涉示意图
我们通过光学系统让光产生干涉,发现在右侧半反半透镜的上下2个面总会有一个干涉相消、一个干涉相涨。这里需要说明一点,当光从光疏介质入射到光密介质反射时,会有半波损失,即会改变π相位,从光密介质入射到光疏介质时,相位不发生变化。所以,总结一下,光干涉本质不是光子的直接湮灭,而是能量的再分配!

图5 干涉动态图(图片来源于网络)
前面我们讨论了干涉的原理,如图5所示,当2个光源到达像面的距离相差半个波长的偶数倍时,就是亮条纹;如果距离相差半个波长为奇数倍时,为暗条纹。好,接下来我们再来看衍射是如何发生的?中学的时候我们就学过,当光通过小孔的时候,光会发生衍射,而且孔越小,衍射现象越明显。

图 6 单缝衍射示意图(图片来源于网络)

图7 单缝衍射原理图(图片来源于网络)
那么,我们再来看衍射光的理论分析图(图7),衍射光在经过小孔AB后会朝各个方向传播,假设衍射光是平行传播的,那么到达像面的是O点,显而易见,到达这个点的衍射光是没有相位差的,自然是亮条纹。接着增大θ角,显然A点衍射光和B点的衍射光达到像面Q点的光程是不一样的,所以我们用半波带法来分割这个衍射光,即光程差为半个波长为宽度视作一个光源,那么AA1可以看做一个子光源,A1A2可以看做一个子光源,自然这2个光源的相位刚好相反,即干涉相消,所以随着θ角的增大,光程差会发生变化,条纹会亮暗相间。接下来回答为什么孔越小,衍射越明显。反一下就是孔越大,衍射现象越不明显。衍射现象明不明显,我们一般是用光的强度来判断。如图7,如果小孔AB可以划分为11个半波带,那么其中10个干涉相消,只剩1个还在,那么这一级应该是亮条纹,能量用面积上来理解就是1/11;如果小孔AB只可划分5个半波带,那么亮条纹能量面积是1/5。所以得出结论:孔越小,衍射越明显。根据这个半波带法,还可以得出另一个结论:当小孔大小不变的情况下,波长越长,被分割的半波带数量越少,自然单个半波带能量面积越大,衍射现象越明显。单缝衍射介绍完毕,接下来就轮到多缝衍射了。多缝衍射显然应该是单缝衍射以及干涉的结合体,所以我们就得到了下面这个图:

图8 多缝衍射原理图(图片来源于网络)
多缝衍射最经典的例子就是光栅。那我们现在以光纤光栅为例,来看看光纤光栅是怎么工作的以及有什么用途。

图9 光栅衍射原理图
图9为光栅干涉衍射原理图,把它代入到光纤中,我们就可以简化成下图:

图10 布拉格光纤光栅原理(图片来源于网络)
根据上一期光纤传感中的光传输原理,不仅需要满足全反射条件,而且需要满足一定的相位条件。这个相位条件,也可以根据图9推导出来,即两束光的光程差要是波长的整数倍才能干涉相涨:
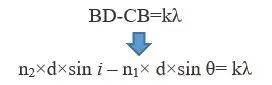
由于衍射光0级和1级的光强相对大一点,所以2级以后的衍射光几乎忽略不计。当取k=1时,我们可以得到衍射光的波长与光栅周期d和折射率、角度有关系。显然,如果要1级衍射光能够在光纤中反向传输,那么光线必须和入射光线要平行(光纤中的相位匹配条件)。根据公式想象一下,我们总会有那么个波长的光线满足这个角度后向传输,这个波长我们就叫做布拉格波长,这种反射式的光纤光栅也叫做布拉格光纤光栅。这里需要再说明下,光其实是很神奇的,各个波长的光都会有各自的衍射光,但是由于其他波长的衍射光没有满足光纤传输干涉相涨的条件,所以就不往1级衍射光这个方向走了,全部往0级衍射光方向传输。问题又来了,光纤中的光居然可以反向传输,那衍射光一定是反向的吗?不一定,根据上面的公式,在波长一定的情况下,显然光栅周期d和角度θ成反比,所以当光栅周期d足够大的时候,我们发现θ角变成正向传输了,如下图所示。传输原理同上,我们同样会得到这么个波长使得其满足光纤中传输的条件,且这个波长传输的角度不再是在光纤纤芯中全反射,而变成了在包层中全反射,这就是包层模的模式。而包层模式的光会在很短距离内衰减损耗掉,所以在光纤的接收端我们得到了除了这个波长的光信号,于是我们也把这种光纤叫做透射式光纤光栅,亦叫作长周期光纤光栅;而布拉格光纤光栅,即反射式光纤光栅也叫作短周期光纤光栅。

图11 长周期光纤光栅原理(图片来源于网络)

图12 (a)布拉格光纤光栅反射谱;(b)长周期光纤光栅透射谱(图片来源于网络)
本文来自何卓铭科学网博客。